Note: If you're hearing about binary tree for the first time (or after a long time), this Introduction to binary tree article will be helpful.
We can perform four basic operations on a binary tree:
Inserting an element
Removing an element
Searching for an element
Traversing the tree
Let's discuss each of the operations in detail.
1. Inserting an element
Given a binary tree and a key, we want to insert the key into the binary tree at the first position available in level order.
Level Order Traversal technique is defined as a method to traverse a Tree such that all nodes present in the same level are traversed completely before traversing the next level.
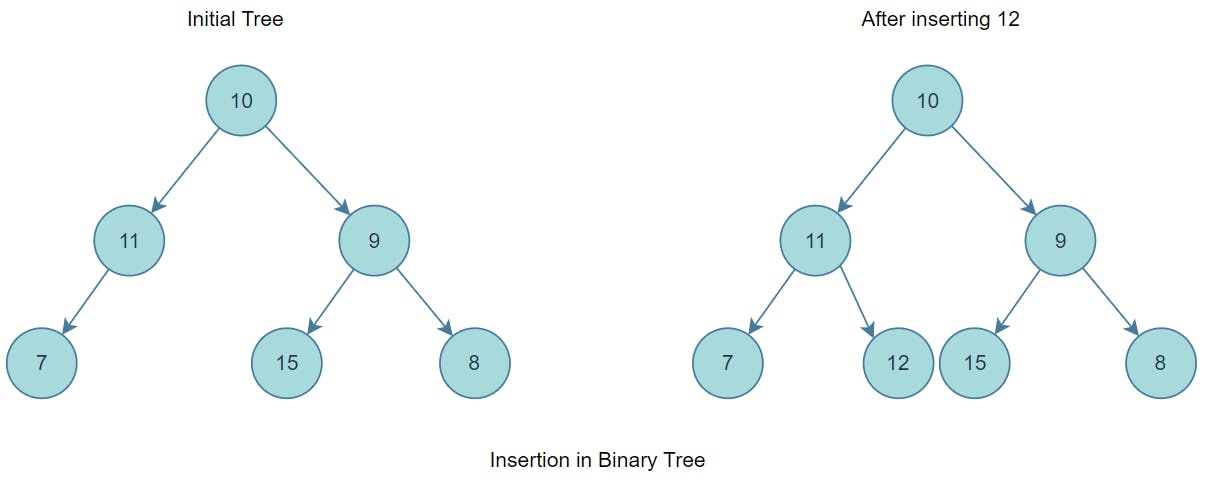
The idea is to do an iterative level order traversal of the given tree using a queue. If we find a node whose left child is empty, we make a new key as the left child of the node. Else if we find a node whose right child is empty, we make the new key the right child. We keep traversing the tree until we find a node whose either left or right child is empty.
# Python program to insert elements in binary tree
class Node:
def __init__(self, data):
self.val = data
self.left = None
self.right = None
def traverse_in_order(self):
if self.left:
self.left.traverse_in_order()
print(self.val, end=' ')
if self.right:
self.right.traverse_in_order()
def insert(self, val):
new_node = Node(val)
q = [self]
# Do level order traversal until we find an empty place
while len(q):
node = q[0]
q.pop(0)
if node.left is None:
node.left = new_node
break
else:
q.append(node.left)
if node.right is None:
node.right = new_node
break
else:
q.append(node.right)
root = Node(10)
root.left = Node(11)
root.left.left = Node(7)
root.right = Node(9)
root.right.left = Node(15)
root.right.right = Node(8)
print("Inorder traversal before insertion:", end=" ")
root.traverse_in_order()
root.insert(12)
print("\nInorder traversal after insertion:", end=" ")
root.traverse_in_order()
Output:
Inorder traversal before insertion: 7 11 10 15 9 8
Inorder traversal after insertion: 7 11 12 10 15 9 8
Complexity Analysis:
Time Complexity: O(V), where V is the number of nodes.
Auxiliary Space: O(B), where B is the width of the tree and in the worst case we need to hold all vertices of a level in the queue.
2. Removing an element
Given a binary tree, we want to delete a node from it by making sure that the tree shrinks from the bottom (i.e. the deleted node is replaced by the bottom-most and rightmost node).
Approach:
Starting at the root, find the deepest and rightmost node in the binary tree and the node which we want to delete.
Replace the deepest rightmost node’s data with the node to be deleted.
Then delete the deepest rightmost node.

# Python3 program to delete element in binary tree
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def traverse_in_order(self):
if self.left:
self.left.traverse_in_order()
print(self.data, end=' ')
if self.right:
self.right.traverse_in_order()
def remove(self, data):
if self.left is None and self.right is None:
if self.data == data:
return None
else:
return root
key_node = None
node = None
last = None
q = [self]
# Do level order traversal to find deepest
# node(node), node to be deleted (key_node)
# and parent of deepest node(last)
while len(q):
node = q.pop(0)
if node.data == data:
key_node = node
if node.left:
last = node # storing the parent node
q.append(node.left)
if node.right:
last = node # storing the parent node
q.append(node.right)
if key_node is not None:
key_node.data = node.data # replacing key_node's data to deepest node's data
if last.right == node:
last.right = None
else:
last.left = None
return root
root = Node(9)
root.left = Node(2)
root.left.left = Node(4)
root.left.right = Node(7)
root.right = Node(8)
print("Inorder traversal before deletion : ", end="")
root.traverse_in_order()
key = 7
root = root.remove(key)
print("\nInorder traversal after deletion : ", end="")
root.traverse_in_order()
Output:
Inorder traversal before deletion : 4 2 7 9 8
Inorder traversal after deletion : 4 2 9 8
Complexity Analysis:
Time complexity: O(n), where n is no number of nodes
Auxiliary Space: O(n), where size of the queue
3. Searching for an element
Given a Binary tree and a node, we want to search and check if the given node exists in the binary tree or not. If it exists, print YES otherwise print NO.
The idea is to use any of the tree traversals to traverse the tree and while traversing check if the current node matches with the given node. Print YES if any node matches with the given node and stop traversing further and if the tree is completely traversed and none of the node matches with the given node then print NO.
"""Python program to check if a node exists in a binary tree"""
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def is_key_exist(self, key):
if self.data == key:
return True
# key not found on current node, recur on left subtree
res1 = self.left.is_key_exist(key) if self.left else None
if res1:
# node found, no need to look further
return True
# node is not found in left, so recur on right subtree
res2 = self.right.is_key_exist(key) if self.right else None
return res2
root = Node(0)
root.left = Node(1)
root.left.left = Node(3)
root.left.left.left = Node(7)
root.left.right = Node(4)
root.left.right.left = Node(8)
root.left.right.right = Node(9)
root.right = Node(2)
root.right.left = Node(5)
root.right.right = Node(6)
for key in [4, 44]:
print("YES") if (root.is_key_exist(key)) else print("NO")
Complexity Analysis:
Time Complexity: O(N), as we are using recursion to traverse N nodes of the tree.
Auxiliary Space: O(N), we are not using any explicit extra space but as we are using recursion there will be extra space allocated for the recursive stack.
4. Traversing the tree
Traversing a tree means visiting and outputting the value of each node in a particular order.
For Inorder, you traverse from the left subtree to the root and then to the right subtree.
For Preorder, you traverse from the root to the left subtree and then to the right subtree.
For Post order, you traverse from the left subtree to the right subtree and then to the root.
Here is another way of representing the information above:
Inorder => Left, Root, Right.
Preorder => Root, Left, Right.
Post order => Left, Right, Root.
Approach: The idea is to place the recursive calls properly as it is done for each of the inorder, preorder and postorder traversal. Here is the python code:
# Binary Tree in Python
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
# Traverse preorder
def traverse_pre_order(self):
print(self.val, end=' ')
if self.left:
self.left.traverse_pre_order()
if self.right:
self.right.traverse_pre_order()
# Traverse inorder
def traverse_in_order(self):
if self.left:
self.left.traverse_in_order()
print(self.val, end=' ')
if self.right:
self.right.traverse_in_order()
# Traverse postorder
def traverse_post_order(self):
if self.left:
self.left.traverse_post_order()
if self.right:
self.right.traverse_post_order()
print(self.val, end=' ')
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
print("Pre order Traversal: ", end="")
root.traverse_pre_order()
print("\nIn order Traversal: ", end="")
root.traverse_in_order()
print("\nPost order Traversal: ", end="")
root.traverse_post_order()
Output:
Pre order Traversal: 1 2 4 3
In order Traversal: 4 2 1 3
Post order Traversal: 4 2 3 1
Complexity Analysis:
Time Complexity: O(N), where N is the number of nodes
Auxiliary Space: O(N), where N is the number of nodes


